The Nash equilibrium is a solution concept in game theory, proposed by mathematician John Nash and used for all non-cooperative games.

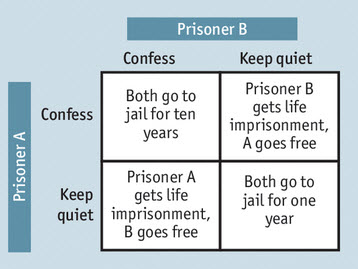The Nash equilibrium is a proposed solution of a non-cooperative game involving two or more players in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing their own strategy.

A group of players are in Nash equilibrium if each one is making the best decision possible, taking into account the decisions of all other players as long as the other players’ decisions remain unchanged. Each player has chosen a strategy, and no player can benefit by changing his or her strategy while the other players keep their strategies unchanged – the group thus is in Nash equilibrium.

This concept is well known today but was groundbreaking back when it was introduced.  It has had profound effects on many aspects of our society.  It revolutionised how traders invest in stock, binary options and other financial instruments.  The Nash equilibrium is the foundation for modern binary options trading and is used by binary brokers to make sure that they always make money.

The finance industry is just one of many industries that have used the Nash equilibrium to maximise the change that they will make money.  Managers in all sectors of our society use the theory to make decisions that avoid risk and maximise profits.

History

Cournot

While the Nash equilibrium was proposed by 20th century mathematician John Nash and is named after him, a version of the Nash equilibrium concept was used as early as 1838 by French philosopher and mathematician Antoine Augustin Cournot in his theory of oligopoly. In Cournot’s theory of oligopoly, each company produces the amount of output that maximizes its own profit. However, the ideal ouput for one company depends on the outputs of others. A Cournot equilibrium occurs when each company’s output maximizes its own profits given the output of the other companies. Today, we call this pure-strategy Nash equilibrium.

Cournot also introduced the concept of best response dynamics in his analysis of the equilibrium’s stability.

Von Neumann & Morgenstern

The type of equilibrium we today refer to as mixed-strategy Nash equilibrium was introduced by John von Neumnann and Oskar Morgenstern in their book “The Theory of Games and Economic Behavior”, published in 1944. However, Neumann and Morgenstern’s equilibrium was limited to t zero-sum game scenarios with a finite set of actions.

Nash

In his article “Non-Cooperative Games”, published in 1951, John Nash defined a mixed-strategy equilibrium for any game with a finite set of actions, and also proved that at least one (mixed-strategy) Nash equilibrium must exist in such a game.

The Nash equilibrium is broader than both Cournot’s equilibrium and the definition of a Pareto-efficient equilibrium. Notably, Nash’s definition makes no judgements about the optimality of the equilibrium being generated. Instead, the modern game-theoretic concept of Nash equilibrium is defined in terms of mixed strategies.

Special circumstances

Game theorists have unveiled that Nash equilibrium makes misleading predictions, or fails to make a unique prediction, in certain circumstances. To overcome these flaws, several refinements of Nash equilibrium have been proposed.

Example: In 1965, German economist Reinhard Selten proposed the refinement subgame perfect equilibrium. This refinement eliminates equilibria that depend on non-credible threats.

In 1994, Nash, Reinhard and Hungarian-American economist John Harsanyi shared the Nobel Memorial Prize in Economics.

This article was last updated on: November 1, 2018